Circulant Matrix In Digital Image Processing
Circulant matrix in digital image processing. An n n matrix is called a circulant matrix if it is of the form 2 In other words a circulant matrix is a matrix where each row below the top row is a cyclic shift of the row immediately above it. An Image may be defined as a two dimensional function f xy where x y. A square matrix in which each row is a circular shift of the preceding row.
We propose a new method for image reconstruction based on circulant matrices. Image Restoration refers to a class of methods that aim at reducing or removing various types of distortions of the image of interest. Nikou Digital Image Processing E12 Block matrices A ij are matrices.
Let be a permutation of the set f1ngde ned as 3 1 1. NR is the circulant matrix with parameters a 1a n. J n 2 j.
Circulant matrices are easy to handle since their products sums and multiplication by scalars are themselves circulant matrices. We represent Hcas the sum of the DIGITAL IMAGE PROCESSING 173 Toeplitz matrix and a matrix D which is highly sparse that circularizes the Toeplitz. Correlation matrices of periodic sequences.
1 Circulant matrices are very useful in digital image processing and the circulant matrix is implemented as CirculantMatrix l n in the Mathematica application package Digital Image Processing. 23 is not the same as inverting the original Toeplitz matrix which it approximates. If γ 1 Classic Wiener filter.
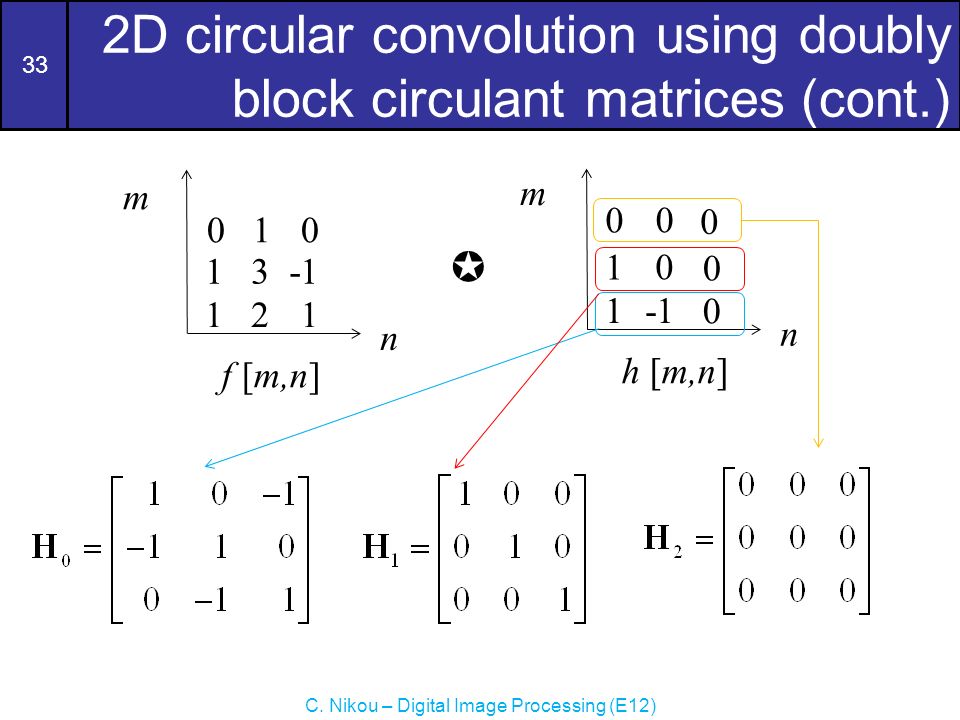
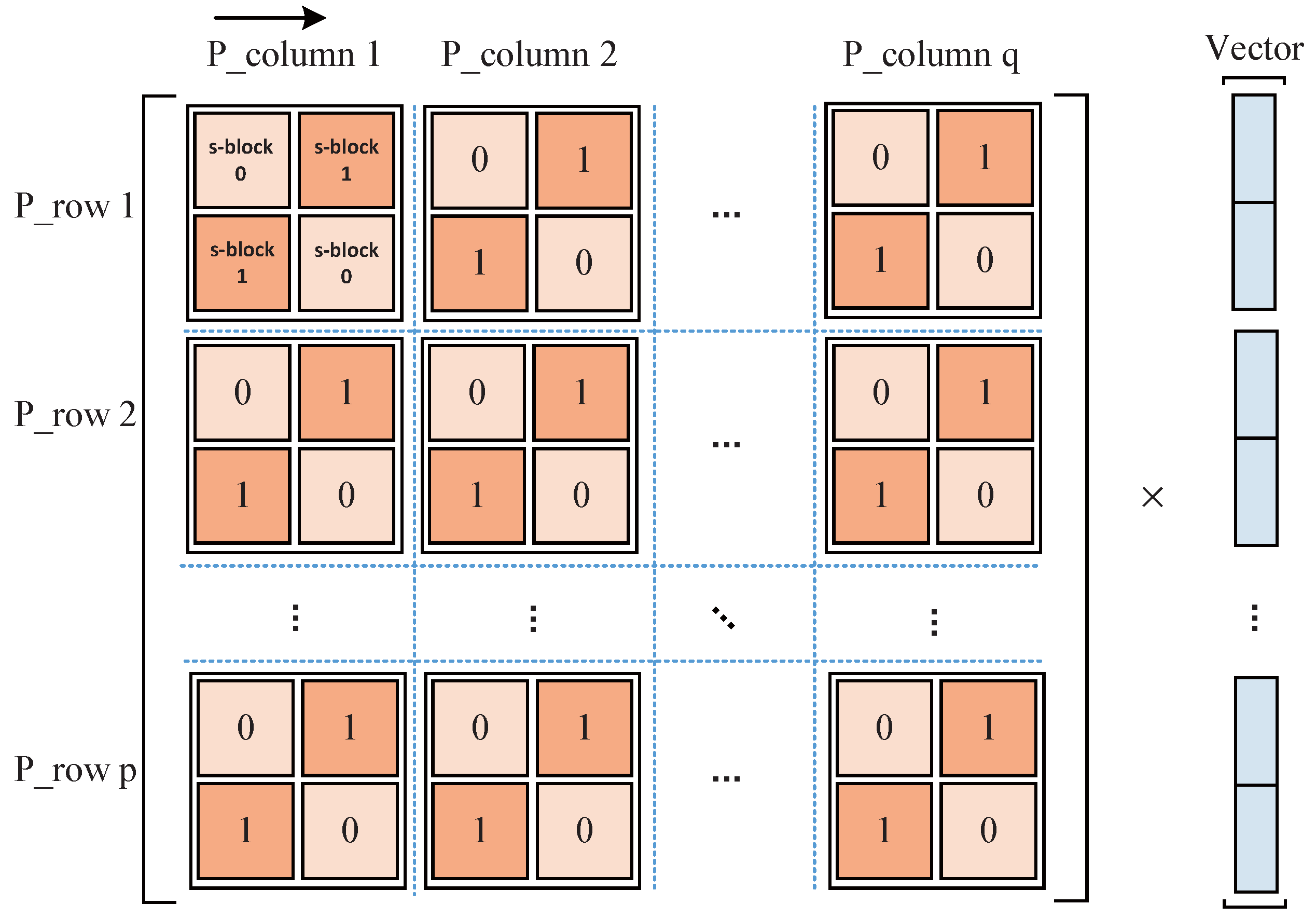
If each individual A ij is also a Toeplitz circulant matrix then A is called doubly block-Toeplitz doubly block-circulant. Digital signal pro-cessing image compression physicsengineering simulations. We denote P 2M nR the matrix with entries p ij such that for any j 1n p j 1 and p ij 0 otherwise.
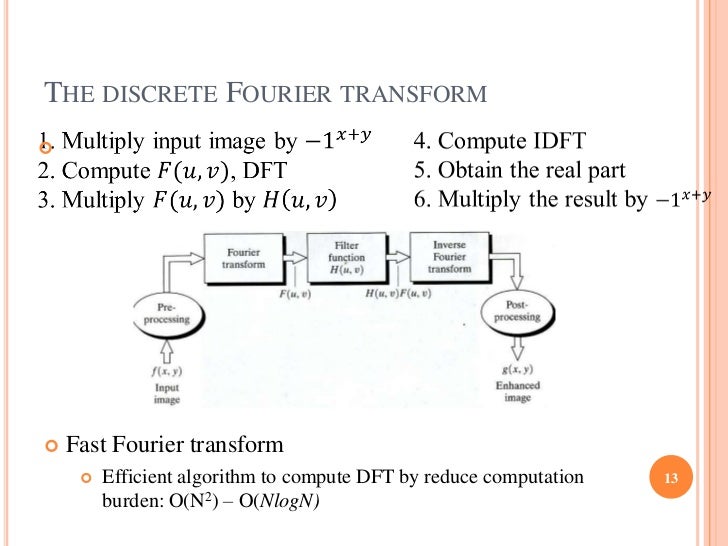
The digital image is N-by-N after zero padding. Implementation Power spectral density is estimated using periodogram Degradation model is designed to be a low pass filter a circulant matrix Iterative Procedure They refer to a class of iterative procedures that successively use the Wiener filtered signal as an improved prototype to update the covariance estimates of the original image as follows.
X is a Nx1 vector with elements x i.
J n 2 j. Notice that Circe I and Circ1 J. An n n matrix is called a circulant matrix if it is of the form 2 In other words a circulant matrix is a matrix where each row below the top row is a cyclic shift of the row immediately above it. If each individual A ij is also a Toeplitz circulant matrix then A is called doubly block-Toeplitz doubly block-circulant. If γ 1 Classic Wiener filter. For example the circulant matrix on the list is given by. G Hf n Linear blur Ideal digitizerdigitizer Restoration f Hn fxy g fˆ. Also called power spectrum or spectral density S f μ ν and S n μ ν Define. Digital Image Processing Image Restoration Part 1 DR TANIA STATHAKI READER ASSOCIATE PROFFESOR IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON.
Let be a permutation of the set f1ngde ned as 3 1 1. If the structure of A with respect to its sub-matrices is Toeplitz circulant then matrix A is called block-Toeplitz block-circulant. Notice that Circe I and Circ1 J. If blur is shift-invariant H is a block-circulant matrix. A square matrix in which each row is a circular shift of the preceding row. Fx is a scalar function of vector xgx is a Mx1 vector valued function of vector x. However the inverse of our circulant approximation in Eq.






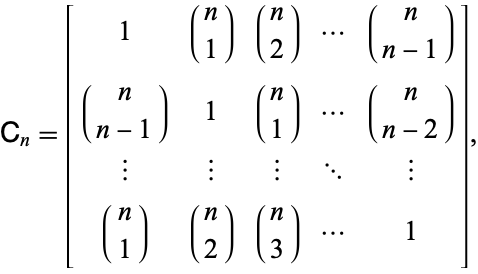

























Post a Comment for "Circulant Matrix In Digital Image Processing"